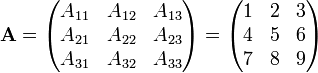Programiranje u C jeziku
-

- LaPommes
- Korisnik
-

- stajpZg
- Korisnik
-

- smayoo
- Moderator
-

- smayoo
- Moderator
-

- LStands4Love
- Korisnik
-

- LaPommes
- Korisnik
-

- LaPommes
- Korisnik
-

- smayoo
- Moderator
-

- jzelko
- Korisnik
-

- smayoo
- Moderator
-

- smayoo
- Moderator
-

- LaPommes
- Korisnik
-

- smayoo
- Moderator
-

- LaPommes
- Korisnik
-

- LaPommes
- Korisnik
-

- smayoo
- Moderator
-

- smayoo
- Moderator
-

- LaPommes
- Korisnik
-

- LaPommes
- Korisnik
-

- LaPommes
- Korisnik
-

- LaPommes
- Korisnik
-

- smayoo
- Moderator
-

- LaPommes
- Korisnik
-

- LaPommes
- Korisnik
-

- smayoo
- Moderator
-

- IgorD
- Korisnik
-

- john_st
- Korisnik
-

- Djipi
- Korisnik
-

- smayoo
- Moderator
-

- IgorD
- Korisnik
Moderatori: Bertone
Vikalica™
Zadnja poruka: pred 12 sati, 15 minuta
- smayoo: RIP Chris Rea...

- VanjusOS: ovo lasersko graviranje izgleda odlično, nikakve naljepnice!
- Bertone: ... i da, mislim da je sad graviranje oko 20€
- Bertone: Lasersko graviranje, baci oko na [link] , ovako izgleda na T14s koji sam nosio kod njih s time da nisam htio baš sve znakove nego samo par osnovnih, tipkovnica je isto bila DE [link]
- jura22: Radije kupi naljepnice. Ima ih na oglasniku: [link]
- Riba: Puno, jer ako se ne varam mora se mijenjati kuciste.
- CoffeePod: Kupio MBP16" M4, al tipkovnica je njemacka. Zna li se koliko bubvrega dode zamjena tipki da mi bude HR?
- Soffoklo: Misliš bravo retardirana EU birokracija
- drpongrac23: Bravooo Apple, super!!!
- m@xym: a evo i pojašnjenja: [link]
- Yonkis: In iOS 26.2, Wi-Fi network synchronization between iPhone and Apple Watch will no longer be available in the EU.
- hal9000: HAHAHAHAHAHA: [link]
- dpasaric: Iskreno, i meni Liquid Glass ide na živce i nije im to trebalo. Srećom barem se na iPhoneu lako ugasi u onim opcijama za invalidne osobe.
- Borisone: Ne znam što su se svi uspuhali oko Liquid Glass, a tragediju od prikaza UI-a na ne-retina ekranima se tolerira više od desetljeća.
- CoffeePod: Dyeovog odlazak je mozda najbolja stvar. Racunam da ce implementirat malo nazad Mavericks draži i da će utišat Liquid Glass gimmick. Apple se stvarno mora sjetiti da ljudi vole Apple upravo radi blenda vrhunskog hardware i software koji je funkcionalna koliko i lijepo izgleda. Liquid Glass je form over function 101.
- Yonkis: Sa novim WApp updateom funkcionalan WhatsApp app na Apple Watchu.
- IgorD: Zašto ne bi bilo istina? O tom se govori danima, neki ljudi slave što je Dye otišao. Trebao si otvoriti temu
- Djuro genijalac: Sve mi se čini da je ovo istina..?
- Djuro genijalac: [link]
- IgorD: ovo je bilo na 17
- IgorD: [link]
- IgorD: Meni radi paste, iPhone Max 15, nije zadnji ios
- smayoo: Ne možeš s iphonea
- Djuro genijalac: Jbm, kak se pastea link u vikalicu?
- Djuro genijalac: Ne znam jel ovo istina, ali....
- Air: Ja sam u Zg, reci što i kada trebaš?
- drlovric: Ima li neka dobra dusa iz Zagreba da mi preuzme hedan mali paket i preusmjeri ga na paketomat ili kakogod u Zupanju?

- smayoo: [link]
- ydrea: @Vanjuška - imamo! Poslao sam ti pp

- drlovric: Akom znate nekoga da prodaje SteamDeck, ja bih to kupio...
- Piko: Zašto WP ? .... ima .... samo ja radim u Laravelu, no WP mi nije stran.. što konkretno treba ?
- dpasaric: Svi otišli u keramičare. Naš ex-voditelj weba radi s mramorom sada.

- Vanjuška: Imamo li na Jabučnjaku ikoga tko je vičan WordPressu i općenito web hokus pokus?
- Riba: Anker ili Baseus i na miru si.
- drlovric: Ja vjerujem Ankeru. Godinama bez problema
- dpasaric: Ne kupuj nikada jeftine punjače za auto, gomila je uništenih iPhonea na taj način.
- Yonkis: ima netko za preporučiti autopunjač a da ima USB C i USB A? Ne vjerujem ovima ovim artiklima od 5€.
- zvone: Vrhunski. Moj prvi OS je 7.5. Digao ga i igrao Sim Tower satima. Kao u stara dobra vremena.
- smayoo: Evo stavio sam ja [link]
- dpasaric: To je vrijedan link, nemoj da se izgubi na Vikalici, imamo u forumu grupu MacOS Classic, pa ostavi tamo da ostane
- IgorD: Da, mogao bih nekom to amjestit full scree da se šokira kad se vrati a komp
- smayoo: hvala!
- drlovric: Ovo je tako cool. Svaka cast!!
- Ender: @IgorD: ovo je sjajno! hvala!
- IgorD: > Infinite Mac is a collection of classic Macintosh and NeXT system releases and software, all easily accessible from the comfort of a web browser
- IgorD: Upravo otkrio: [link]
- m@xym: RIP Deajn Ristanović, jedan od rijetkih koji je postao legenda još za svog života (barem nama koji smo pratili same početke kompjuterizacije u bivšoj državi.
- smayoo:

- IgorD: Računari itd. RIP
- Yonkis: Zar Apple nije mogao napraviti bolji emoji za miša, tj za magic mouse?
Prijava
Prisutni jabučari
^SuperUnknown^, Anonimci (498)
Novo na Jabučnjaku
Teme
- Mac OS X: Opencore Legacy Patcher i Sonoma na Mac Pro 6.1 | 05.07.2025 | 22:25 | Riba
- Razno: Ukrajina | 25.02.2022 | 17:47 | Ender
- Razno: Automobili (i sve oko toga...) | 24.06.2018 | 09:49 | cariblanco
- Hardver: Grupno naručivanje BlueSCSI pločica | 20.12.2025 | 22:14 | lukeisok
- Softver: Hidden space, nestala aplikacija ... | 19.12.2025 | 18:26 | smayoo
- Jabučnjak: iParty 2025 | 27.11.2025 | 22:27 | hal9000
- Softver: program naveden u login items se ne pali pri login | 22.12.2025 | 00:11 | smayoo
- Razno: Trump i Musk - MAGA ili MASA | 10.03.2025 | 06:06 | Yonkis
- Hardver: Mac Pro 2019 (7,1) | 18.11.2025 | 14:51 | dpasaric
- Razno: Windows 11 i TPM čip | 02.11.2025 | 10:57 | dpasaric
- Razno: Umjetna inteligencija | 22.12.2022 | 00:23 | dpasaric
- Grafika: Font za naslov dječije knjige | 18.12.2025 | 15:57 | drpongrac23
Poruke
- Mac OS X: Opencore Legacy Patcher i Sonoma na Mac Pro 6.1 | 23.12.2025 | 00:54 | Riba
- Razno: Ukrajina | 22.12.2025 | 23:05 | Ender
- Razno: Ukrajina | 22.12.2025 | 23:03 | Ender
- Mac OS X: Opencore Legacy Patcher i Sonoma na Mac Pro 6.1 | 22.12.2025 | 22:30 | dpasaric
- Razno: Ukrajina | 22.12.2025 | 22:25 | dpasaric
- Razno: Automobili (i sve oko toga...) | 22.12.2025 | 22:24 | cariblanco
- Mac OS X: Opencore Legacy Patcher i Sonoma na Mac Pro 6.1 | 22.12.2025 | 21:32 | Riba
- Hardver: Grupno naručivanje BlueSCSI pločica | 22.12.2025 | 21:08 | lukeisok
- Razno: Automobili (i sve oko toga...) | 22.12.2025 | 20:58 | cariblanco
- Razno: Automobili (i sve oko toga...) | 22.12.2025 | 18:14 | Bertone
- Softver: Hidden space, nestala aplikacija ... | 22.12.2025 | 14:18 | smayoo
- Razno: Automobili (i sve oko toga...) | 22.12.2025 | 14:16 | smayoo
Članci
- Hardver: Mac Pro - Pimp My Ride!
- Hardver: Budućnost Intela na Macu
- Hardver: MacBook Pro 14" - kreativna Formula 1
- Hardver: iMac M1 24" - dobar dan!
- Hardver: Mac Pro 2019 - obiteljsko stablo: djed, otac i sin
- Audio: Apple HomePod - obris domova budućnosti
- Igre: Daleko Lone jedri!
- iPhone: JM Elektronika - alternativa Appleovu servisu
- Hardver: NVMe dogradnja za Mac Pro
- Softver: Tri korisna alata
- Hardver: Čekajući novi Mac Pro
- Softver: Docker - virtualna okolina za vaše aplikacije
Oglasi
- Potražnja/Potražnja: ADB tipkovnica i miš | 22.12.2025
- Ponuda/Ponuda: Razni dijelovi za Mac Pro 5,1 | 9.12.2025
- Potražnja/Potražnja: KUPUJEM : Neispravan iPhone 12 mini ili ekran | 4.11.2025
- Potražnja/Potražnja: Kupujem Macbook Pro 2012+ | 7.10.2025
- Ponuda/Ponuda: Satechi M1 Bluetooth Wireless Mouse - Space Gray | 5.10.2025
- Potražnja/Potražnja: PowrmacG4 DP | 2.10.2025
- Ponuda/Ponuda: Mac Pro 2009 | 19.9.2025
- Ponuda/Ponuda: Apple Macbook Pro, 16”, i9, 1TB ssd, u savršenom stanju | 27.8.2025
- Potražnja/Potražnja: kupujem Magic Mouse 2 | 20.8.2025
- Ponuda/Ponuda: Apple Mac Pro 7,1 2019 12-Core 32 GB 1 TB Tower | 14.8.2025
- Ponuda/Ponuda: MacBook Air 2017 | 15.7.2025
- Ponuda/Ponuda: Apple iMac 27" Retina 5K (2017) – i5 / 64 GB RAM / 1 TB SSD | 6.7.2025
- Ponuda/Ponuda: Keychron K8 | 26.6.2025
- Ponuda/Ponuda: HomeMatic - smart home oprema | 26.6.2025
- Ponuda/Ponuda: G5 2 x 2,66 Mhz Dual-Intel Xeon | 17.6.2025
- Ponuda/Ponuda: iMac late 2011 | 2.6.2025
- Ponuda/Ponuda: Apple Time Capsule 802.11n A1254 2000 GB | 28.4.2025
- Ponuda/Ponuda: Apple Time Capsule 802.11n A1254 500 GB | 28.4.2025
- Ponuda/Ponuda: Macbook Air i5 16GB RAM, 2019. godina, 128 GBSSD | 19.4.2025
- Potražnja/Potražnja: Kupujem 49mm Black Titanium Milanese Loop - Large | 24.3.2025
- Ponuda/Ponuda: Mac Mini M1, 512 gb, 16 gb + dock i ssd 2tb | 3.3.2025
- Ponuda/Ponuda: Mac Pro 2013 6.1-3,5 GHz, 64 GB RAM, 1TB SSD, 2x AMD D700 | 31.1.2025
- Ponuda/Ponuda: Mac Pro i iPad Air | 27.1.2025
- Ponuda/Ponuda: Mac mini 2018 / i7 6C 3.2 GHz / 16GB / 512GB SSD | 24.1.2025
Komentari
- Iz ljubavi: Dario mi se jučer pohvalio da je nabavio novi Reason... | 28.11.2025 | 08:21 | dpasaric
- Mac Pro - Pimp My Ride!: Svakako QS ako ne postoji mogućnost testa prije kupnje!... | 18.11.2025 | 14:07 | dpasaric
- Mac Pro - Pimp My Ride!: I? Onda? ES ili QS? | 18.11.2025 | 12:58 | hal9000
- Mac Pro - Pimp My Ride!: Danas sam odradio veliki upgrade članka! :) Naime,... | 18.11.2025 | 12:38 | dpasaric
- MacBook Pro M4 16" - radna stanica u ruksaku: Zaista jest. Osim što nikad ne uključuje ventilatore... | 13.10.2025 | 13:56 | EPC
- Dobili smo više prostora, ali Siri je i dalje na godišnjem odmoru: https://www.bug.hr/mobiteli/iphone-ce-za-svoj-20-rodjendan-znacajno-promijeniti-dizajn-48920 | 09.10.2025 | 15:00 | ZoPaj
- Iz ljubavi: Ja nisam naročiti fan žanra, ali pratim ga u okvirima... | 05.10.2025 | 19:02 | smayoo
- Iz ljubavi: Cijeli zivot sam u elektronskoj glazbi. Radio sam davno... | 05.10.2025 | 16:10 | drlovric
- Iz ljubavi: [quote name="dpasaric"]Dario, evo, sada i jedno neformalno... | 05.10.2025 | 14:28 | hal9000
- Iz ljubavi: Dario, evo, sada i jedno neformalno veliko hvala od... | 05.10.2025 | 14:22 | dpasaric
- Dobili smo više prostora, ali Siri je i dalje na godišnjem odmoru: Možda ne spada u ovaj post ali se bavi novim uređajima... | 30.09.2025 | 15:38 | Yonkis
- Dobili smo više prostora, ali Siri je i dalje na godišnjem odmoru: Ni kamere nisu neki napredak. Mislim da smo dosegli... | 26.09.2025 | 07:52 | drlovric